|
|
|
||
You should make JavaScript available to read this page.
Please enable the execution of JavaScript!

























































































































































































































































































【オリジナル理論で拡張現実センサを作ってみよう】~トランジスタ技術【増刊】『今すぐ使える パソコン計測USBマイコン基板』の付録で作る~ |
||

|
【リンクフリー】 私設研究所ネオテックラボ Neo-Tech-Lab.co.uk 【記載者】 【私設研究所Neo-Tech-Lab】 上田 智章 |
作成日 2012/02/07 |
ここにチェックボックス型外部コンテンツ・メニューが入ります。 | ||
|
|
|
||
【HTML5+JavaScript+AR】【円形マーカー検出拡張現実センシング】 |
|||
 Interface2013年10月号 3次元グラフィックスはWebGLを使わず、Canvas用NTL3D.jsを使用しています。 |
障害物でマーカーの一部が欠けても検出可能なオリジナル・アルゴリズムで開発。アルゴリズムの動作原理はサポートページで詳細を記述・説明しています。  |
Kinectのデプスイメージから円形マーカーの中心座標を推定し、半径と法線ベクトルを取得する理論も記載。 【サンプル・プログラム】 【対応ブラウザ】最新版Google Chrome, FireFox, Opera ●『円形マーカーによる距離測定デモ』 ●『回転するピラミッド拡張現実表示』 ●『マーカー移動履歴の表示』 ★マーカー半径750mm, 黒枠太さ15mm~30mmで適当に作ってみて下さい。 |
|
【以下は過去記事の残骸です。最新版は上記記事URLにて記載】 |
【ARToolKitの中身の処理を考察してみる】記載日 /2012/02/06/ 03:00以下は、ARToolKitのソースは読まずに(だって人のソースを読むのは面倒だし。)、中でやっていそうな処理を考察してみたメモです。 GPLライセンスとか確かに非商用では自由だけど、米国基準で全て支配されるのは如何なものか? 例えば、MicrosoftのXBOX360用のKinectセンサのキャプチャー画像を利用してARToolKitを使おうとすると、 Microsoftの権利とGPLがバッティングしそうだ。 折角ソフトを開発してもKinect SDKのところはブラックボックスで不明だし、全てのソースを公開できないもの。 やはり面倒でも自前のアルゴリズムでマーカー検出する必要性はありそうだ。 そんなわけで、自力であれこれ考えてみることにしました。 何か技術的な要素を追っかけていれば新しいアイディアも湧いてくるかも。 ARToolKitの中身の処理は恐らく以下のような処理ではないかと思う。 ①濃淡画像の取得(DirectShow利用) これはKinectセンサを使う場合には悩む必要はないし、Windows以外ならいくらでも方法はある。 DirectShowを使わなくても、直接、CCDカメラからイメージを読み出す方法もあるし。 私の場合はKinectセンサで骨格追尾とマーカー検出の両方を同時に使いたいので、 KinectセンサのColorImageFrameから画素データを取得する。 ②濃淡画像から直接、輪郭線を得る(可能な限り孤立点は除去) 20年前の信号処理方法を流用して、太い黒線を検出する方法を適用してみました。 +1と-1の値を持った矩形窓を用いる方法です。 (例えば、心電図のR波を検出する場合の応用例は特許2031679[H8.3.19]) この処理が終了した段階で、マーカー存在領域のスキャンライン単位の左端画素と右端画素(エッジ)の点座標リストが作成されている。 ここまではオリジナルアルゴリズムでコーディングしてみた。     注)右側のイメージは作成する必要はなく、動作確認の目的で作成した。 ③矩形マーカーを構成する4頂点を探索する 輪郭線集合の存在領域(xmin,ymin)-(xmax,ymax)の中央点((xmax+xmin)/2, (ymax+ymin)/2)と各輪郭画素(xj, yj)までの距離の2乗値を求めれば、 映像が完全なら4つの極大値が見つかるはずです。この極大値を示す画素の座標がマーカーを構成する4頂点のはずです。 とは言え、中央点から線分に垂線を下した場合に線分内に足が乗らない場合には回転などが必要なケースもあるので、 さらにアルゴリズムを煮詰める必要があります。 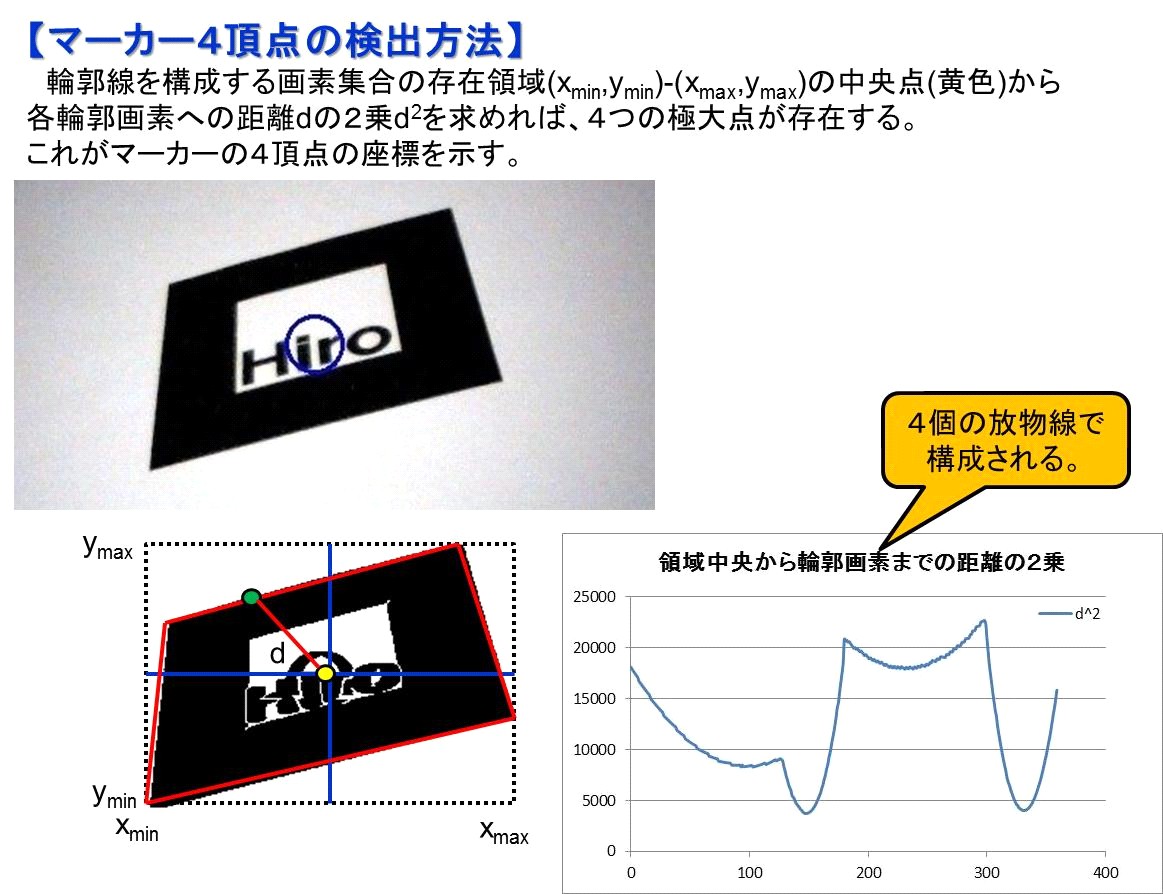 【頂点検出をロバストにする工夫】 画像が不鮮明であったり、指でマーカーの一部が隠れ完全に映っていない場合にでも ロバストに検出する方策として、見つかった極大値間の画素座標データから 私オリジナルの推定アルゴリズム(Base Transition Rule)で、直線方程式を高精度に得ることができます。 本質的に最小2乗法なので、全てのデータを処理する必要は全くなく、 飛び飛びのランダムな数個の画素からでも直線方程式のパラメータの推定を行うことができます。 4直線の交点座標はマーカーの4頂点であるはずです。 この方法は、1つのパラメータに関して誤差評価関数Eを整理すると常に放物線になっており、 その誤差の極小値は常に放物線の軸値であることを利用しています。 下の例は未知数1個の場合の例ですが、線形系なら何個でも処理することができる方法です。 実際の処理では、y=ax+bの2つの未知数を求めています。(図や式の導出はそのうち作成します。) 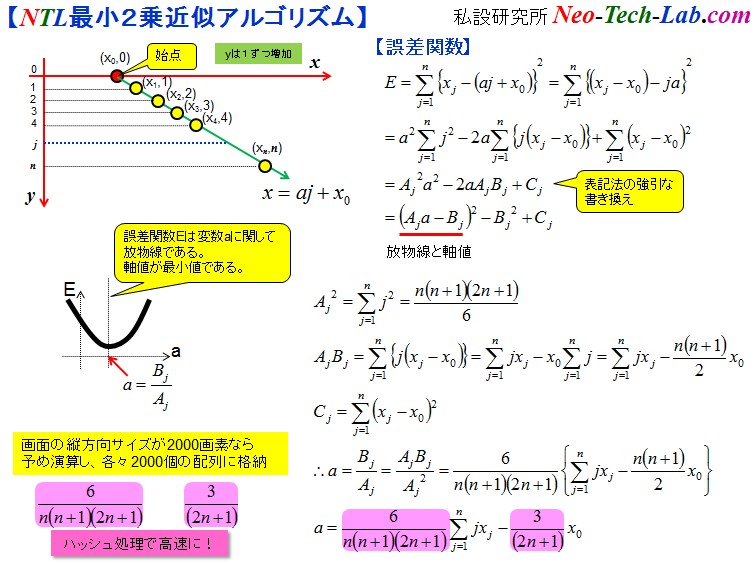 ④抽出線分の4頂点で囲まれる領域からテクスチャーマッピングで画素を読み出して、 マーカーと同じ画素数の正方形領域のイメージを得る。 ⑤切り出したイメージと登録マーカー画像を90度単位に回転させた4パターンを比較。マーカーともっとも一致するパターンを求める。 これによって、キャプチャ画像の輪郭領域の各頂点座標とマーカー頂点の対応がつく。 ⑥透視変換マトリックスの逆行列を求め、スクリーン座標からマーカーの3次元座標を得る。 マーカーの直交2辺の3頂点座標から外積を求めれば法線ベクトルが得られる。 次の節で最小2乗法の独自アルゴリズム(Base Transition Rule)を公開する。 |
【太線枠抽出で用いた高速フィルタ:矩形波相関トリガ法】記載日 /2012/02/06/ 03:00この矩形波相関トリガ法は、0~255の符号なし濃淡情報を-128~+127の符号付き情報に変換して、 白(正)領域と黒(負)領域の境界点を相関処理により抽出するアルゴリズムです。 下記に記載の通り、高速化のために、毎回、相関値の差分計算を行う低演算負荷の方法を採用しています。 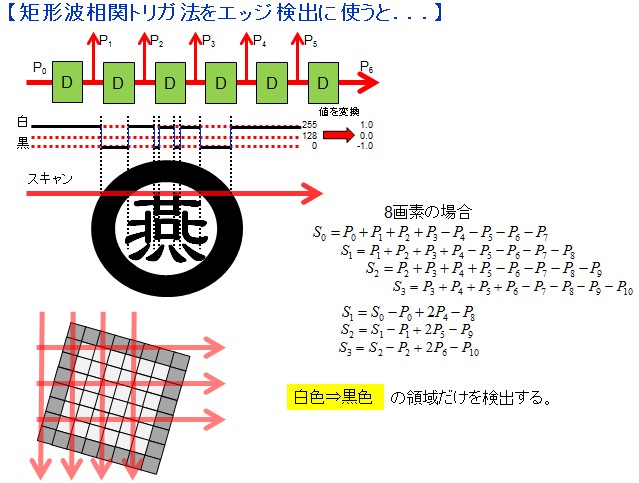 |
■以下はアルゴリズムをテストする目的でExcel VBAツールでコーディングしたもの。【メインの一部】
Nx = MyPic1.Header.Nx
Ny = MyPic1.Header.Ny
BuildBitMap Nx, Ny, MyPic2 '【MyPic2を作成】
BuildBitMap Nx, Ny, MyPic3 '【MyPic3を作成】
nScan = 0
ReDim XL(Ny - 1), XR(Ny - 1)
For j = 0 To Ny - 1
initFilter '【フィルタ初期化】
For i = 0 To Nx - 1
P = Filter(MyPic1, i, j)
DrawPixel MyPic2, i, j, P
Next i
If AR_OnFlag Then
For i = Nx - 1 To AR_XOn Step -1
DrawPixel MyPic2, i, j, MyPic2.White
Next i
End If
If wXL >= 0 Then
Sheet3.Cells(20 + nScan, 2) = j
Sheet3.Cells(20 + nScan, 3) = wXL
Sheet3.Cells(20 + nScan, 4) = wXR
nScan = nScan + 1
End If
Next j
CreateBitMapFile MyPic2, dFileName
Image2.Picture = LoadPicture(dFileName)
【フィルタ部】
Private AR_SumR As Integer
Private AR_SumG As Integer
Private AR_SumB As Integer
Private AR_FIFO_R() As Integer
Private AR_FIFO_G() As Integer
Private AR_FIFO_B() As Integer
Private AR_Ptr0 As Integer
Private AR_Ptr1 As Integer
Public AR_Nw As Integer
Public AR_Nw2 As Integer
Private AR_Th As Integer
Public AR_XOn As Integer
Public AR_XOff As Integer
Public AR_OnFlag As Boolean
Private AR_J1 As Boolean '【左端エッジ】
Private AR_J2 As Boolean '【右端エッジ】
Private AR_J3 As Boolean '【ステータス】
Public wXL As Integer '左端
Public wXR As Integer '右端
Public nScan As Integer '検出データ数
Private XL() As Integer '左端リスト
Private XR() As Integer '右端リスト
Public Sub initFilter()
Dim i As Integer
AR_Nw = 10 'FIFO段数 30
AR_Th = AR_Nw * 20 'しきい値
AR_Nw2 = AR_Nw \ 2 '検出厚み
AR_Ptr0 = 0 'FIFOポインタの初期化
AR_Ptr1 = AR_Nw2 'FIFOポインタの初期化
AR_SumR = 0
AR_SumG = 0
AR_SumB = 0
ReDim AR_FIFO_R(AR_Nw - 1), AR_FIFO_G(AR_Nw - 1), AR_FIFO_B(AR_Nw - 1)
For i = 0 To AR_Nw - 1
AR_FIFO_R(i) = -128
AR_FIFO_G(i) = -128
AR_FIFO_B(i) = -128
Next i
AR_OnFlag = False
AR_J1 = False
AR_J2 = False
AR_J3 = False
wXL = -1
wXR = -1
End Sub
Public Function Filter(cg As NTL_BitMap, x As Long, y As Long) As RGB24bitPixel
Dim w0 As Integer, w1 As Integer, w2 As Integer
Dim P As RGB24bitPixel
P = GetPixel(cg, x, y) '指定座標から画素情報を読み出す
w0 = CInt(P.Red) - 128 'signed int(-128~127)に変換
w1 = CInt(P.Green) - 128 ' 暗:-128
w2 = CInt(P.Blue) - 128 ' 明:127
AR_SumR = AR_SumR - w0 + 2 * AR_FIFO_R(AR_Ptr1) - AR_FIFO_R(AR_Ptr0)
AR_SumG = AR_SumG - w1 + 2 * AR_FIFO_G(AR_Ptr1) - AR_FIFO_G(AR_Ptr0)
AR_SumB = AR_SumB - w2 + 2 * AR_FIFO_B(AR_Ptr1) - AR_FIFO_B(AR_Ptr0)
AR_FIFO_R(AR_Ptr0) = w0
AR_FIFO_G(AR_Ptr0) = w1
AR_FIFO_B(AR_Ptr0) = w2
AR_Ptr0 = AR_Ptr0 + 1: If AR_Ptr0 = AR_Nw Then AR_Ptr0 = 0
AR_Ptr1 = AR_Ptr1 + 1: If AR_Ptr1 = AR_Nw Then AR_Ptr1 = 0
AR_J1 = (AR_SumR > AR_Th) And (AR_SumG > AR_Th) And (AR_SumB > AR_Th) '【左端エッジ】
AR_J2 = (-AR_SumR > AR_Th) And (-AR_SumG > AR_Th) And (-AR_SumB > AR_Th) '【右端エッジ】
If AR_OnFlag Then '【FlagがOnのとき】
AR_XOff = x
wXR = x
If AR_J3 Then '【右端エッジ検出時】
If AR_J2 = False Then
AR_OnFlag = False
AR_J3 = False
End If
Else '【右端エッジ出現待ち】
If AR_J2 Then
AR_J3 = True
End If
End If
Else '【FlagがOffのとき】
If AR_J1 Then '【左端エッジ検出】
AR_OnFlag = True
AR_XOn = x
AR_XOff = x
AR_J3 = False '【右端エッジ未検出】
If wXL = -1 Then
wXL = x '最左端座標を記録
End If
End If
End If
If AR_OnFlag Then P = cg.Black Else P = cg.White
Filter = P
End Function
|
【Hough変換って、とっても面倒そうなのでオリジナルアルゴリズムを考えてみました】記載日 /2012/02/07/ 02:00キャプチャー画像からマーカーの存在する領域を切り出した後、4頂点座標を抽出する必要があります。 検索してみると、Hough変換というのを使っているらしいが、既存アルゴリズムはいろいろ問題があるらしい。 ならオリジナルを作ってみようと思い、20年程前に考案した最小二乗アルゴリズムをこの問題に適用してみました。 Base Transition Ruleと呼んでいます。 画素(x0,y0)を始点とし、スキャンライン毎に(x1,y1),(x2,y2),(x3,y3),(x4,y4),・・・・・・・・・・・・・・,(xn,yn)の画素を 最小2乗誤差で通過する直線の方程式を求め、n+1番目の画素(xn+1,yn+1)を1画素以内の誤差で通過できなければ、 (xn,yn)をコーナー(頂点)と考える方法を取ります。 但し、最小二乗近似のアルゴリズムはNTL特製アルゴリズムです。 y1=y0+1, y2=y1+1, y3=y2+1,・・・・・・・・・・・・・・とスキャンライン単位に1ずつ増加する性質を利用します。 理論式を以下に示します。 昔、高校で習った数列の知識が本当に役に立つとは驚きです。 2種類の係数は予めハッシュテーブルを作成しておきます。 またΣの部分は前回までの演算値にj・xjを加算するだけです。 ARToolKitを自作する自信が湧いてきました。 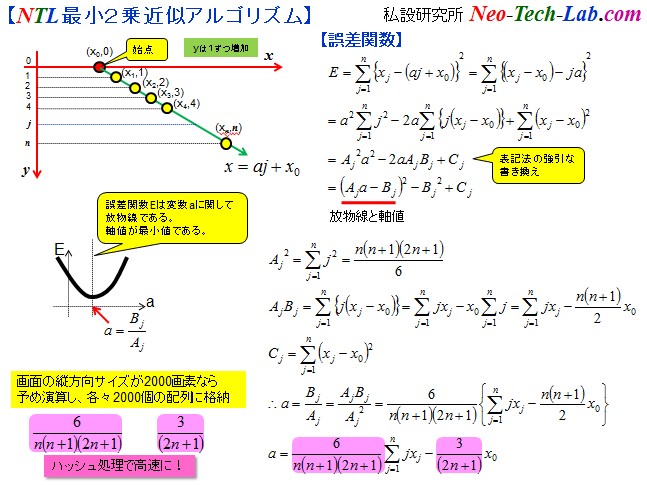  ちなみに、途中が欠落した不連続な点集合を直線近似する場合には、以下のアルゴリズムを用います。 新規な点を集合に加えても、差分を追加計算すればよいことがわかりますよね? 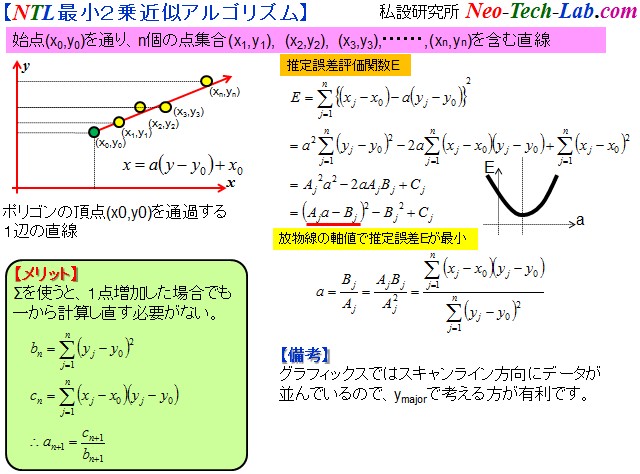 |
【円形マーカーのオリジナル検出アルゴリズムを考えて試作を完了】記載日 /2012/02/23/ 18:47キャプチャー画像から円形マーカーを高速検出するアルゴリズムも考案し、動作を確認しました。 Kinectセンサのキャプチャーを使い、楕円形に歪んだマーカーのリアルタイム検出をしています。 Hough変換の線分検出より速く動作しますし、何よりロバストです。 数学アルゴリズムの優位性がもろに結果に反映されました。 全ての画素を舐めなくても検出できるのが強みです。 既にプライベート動画も作成。 ただ、皆さんに内容を公表するのは、夏(7月?)になりますけどね。 守秘義務契約締結している方々にだけ、結果を開示しています。 ここまでできたら、以前にほったらかしにしている1カメラモーションキャプチャーも可能なのではないかと思えます。 |