【本サイトのご利用指針】
当サイトはSPAM対策等のためJavaScriptを使っています。
JavaScriptの実行を可能な状態にしてご利用下さい。
Please enable the execution of JavaScript!





























「たった２４時間でマスターできる電子回路技術」

【ディジタル系電子回路の基礎】　　(2時間目)
　 　 【リンクフリー】　私設研究所ネオテックラボ Neo-Tech-Lab.co.uk
【記載者】 【私設研究所Neo-Tech-Lab】　上田 智章 		作成日 2009/01/08
最終更新日 2009/06/16
ここにチェックボックス型外部コンテンツ・メニューが入ります。



【ブラウザはGoogle Chrome】

●最新版ダウンロードはこちら

【お知らせ】

現在、特にお知らせする事項はありません。
【まえがき】
　　何かパソコンに接続する計測機器を開発しようとすると、技術者の分業化が進んでしまっているために大掛かりなプロジェクトになりがちです。世の中の大半の企業では、ソフト屋（アプリケーション、組み込み）、ハード屋（アナログ、ロジック設計、マイコン、電源）、さらには基板屋（アートワーク）までと、細かく分業化が進んでいます。ちょっとした機器開発に４、５名のエンジニアが必要になることもあります。人が増えると意思疎通に必要な会議時間も増え、開発期間も長くなってしまいます。当然、開発費は膨らみます。世界的に不景気なご時世に、このような大型開発プロジェクトはもうあり得ないと思いませんか？
　　ではどうすればよいのか？答えは共有の知識を持ったHyper-Generalistを大量生産することです。
　　電子回路技術（ハードウェア、ソフトウェアとも）の未経験者がシステム設計・開発に必要なエッセンスを修得するのに必要な時間は恐らくたったの２４時間程度だと思います。三日坊主という言葉がありますが、１日８時間なら三日坊主にならずにすむでしょう？アナログ系電子回路の基礎 (１時間)、ディジタル系電子回路の基礎（１時間）、・・・・・と順次まとめていく予定です。（記事を書く方は三日坊主になる可能性大ですが．．．）

　　本編では、「ディジタル系電子回路の基礎」について紹介します。内容は、取りあえずCPLD & FPGAの設計ツールで提供されている基本マクロ・ライブラリの回路の動作を理解するのに必要な知識程度です。 ライブラリをただ使うのと理解するのは全く次元が違います。ただ使うだけだと高速な回路設計が行えないだけでなく、必要以上に多くのロジック・エレメント（LE : Logic Element）を使ってしまうなどの弊害があります。そこで中身を理解しておく必要があるのです。
【Index】
　■基本ゲート・ロジック (Basic Gate Logic)
　　■コンバータ (Converter)  ■インバータ (Inverter)  ■シュミット・トリガ　(Schmidt Trigger)  ■バッファ (Buffer)
　　■AND (論理積)　■NAND　■OR (論理和)　■NOR　■XOR (exclusively OR 排他的論理和)　■XNOR
　　■VCCとGND(グランド)　■論理の等価変換法について (ド・モルガンの公式)
　　■入出力ピン (Pin)　■ピンとバッファ　■デコーダ (decorder)
　■INV-AND-OR-treeを理解せよ！
　　■セレクタ　■プライオリティー・エンコーダ　■XORとINV-AND-OR-tree
　　■加算器 (adder)  ■高速加算器を作るためのキャリー・ルック・アヘッド回路 (Carry Look Ahead)
　　■インクリメント (increment)  ■ディクリメント (decrement)
　■レジスタの活用
　　■RSフリップ・フロップ　■レジスタとラッチ (registerとlatch)
　　■これだけは押さえておきたいレジスタのバリエーション
　　■非同期カウンタとその欠点　■同期式カウンタ（アップ・カウンタとダウン・カウンタ）
　　■シフト・レジスタの構成法とその用途　■ステート・マシン
１．基本ゲート・ロジック
　　CPLDやFPGAの設計で重要なのはINV-AND-OR-treeとレジスタです。これを使いこなすために必要な基礎知識について紹介します。
1.1) コンバータ (Converter)
 　図１に示すように入力論理と出力論理が一致している要素です。実際にはICの入力、出力の電圧レベルを変換するバッファにしか用いられることはありません。右図のように三角形のマークを使います。
　通常のロジックICでは電源電圧とグランドレベルの中間電位をしきい値(スレシホールド：threshold)としてそれより低い電圧を"0"(Low)、高い電圧を"1"(High)とします。
　40年程前に標準ロジックIC (SN74シリーズ)が市販されていた頃は電源電圧は５Vでしたが、CMOSロジックではロジック・レベルが変化するときに電流が消費され、しかも電圧スイング幅が小さい方が高速に動作可能なので、低消費電力化と高速化が進むにつれ、電源電圧も3.3V, 2.5V, 1.8V, 1.5Vと次第に低電圧で動作するロジックが増えてきています。これら論理電圧の異なるデバイスを接続するにはコンバータを通す必要があります。多くのCPLDやFPGAには何種類かのロジック・レベルに対応したデバイスが用意されています。　		 【図１】コンバータ (Converter)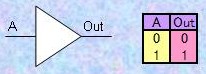
1.2) インバータ (Inverter)
　図２に示すように入力論理と反転した論理を出力するします。NOTとも呼ばれます。コンバータの三角形シンボルに白丸○シンボルが入力側あるいは出力側に付いていることで論理の反転を示します。大事なのは三角形ではなく、シンボル○です。
　ところで、シンボル○を「入力が"0"のとき」と頭の中で唱えるようにしておくと後の理解が容易です。		 【図２】インバータ (Inverter)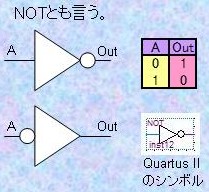
1.3) シュミット・トリガ (Schmidt Trigger)
　IC外部の信号には大きな電圧ノイズが重畳している場合があります。ひとつのしきい値(threshold level)で論理を変換してしまうと、実際には"0"(Low)から"1"(High)に変化しているだけなのに何回も"0"と"1"の間を往復するチャタリングのような現象が起こってしまいます。そこで、"0"→"1"のHighレベル認識用のしきい値と、"0"→"1"のLowレベル認識用のしきい値を２つ持ったシュミット・トリガと呼ばれるデバイスがあります。
通常のシュミット・トリガは
　　Highレベル認識用のしきい値VH　＞　Lowレベル認識用のしきい値VL
となっているため、一度Highになるとかなり電圧が下がるまでLowレベルにはなりません。
CMOSデバイスでは
　　Highレベル認識用のしきい値VH　　≒　電源電圧の2/3
　　Lowレベル認識用のしきい値VL　　≒　電源電圧の1/3
となっています。このような特徴をヒステリシス特性とも言います。　
　通常しきい値が１つの通常のコンバータと区別するため、図３に示すようなヒステリシス特性マークを三角形に加えた記号を使います。

【図３】シュミット・トリガ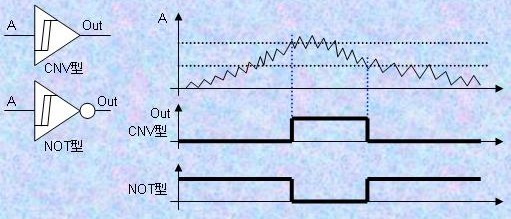
1.4) バッファ (Buffer)
　実は論理レベルは"0"状態と"1"状態以外に"Z"(ハイ・インピーダンス High Impedance)状態の３状態(3-state)が存在しています。ロジック・デバイスの出力には図４の[A], [B], [C]に示すようにグランド側と電源側に接続された２個のスイッチング・デバイスが使われています。"1"(High)を出力するときは電源側のスイッチをON、グランド側のスイッチをOFFにします。反対に"0"(Low)を出力するときは電源側のスイッチをOFF、グランド側のスイッチをONにします。そして、"Z"状態は両方のスイッチをOFFにして『接続しない』状態を作って実現します。"Z"状態は１本の信号線(ライン)を複数のデバイスで時分割で使用する場合に必要な状態です。ラインを使用しない他のデバイスはデータを出力しないように両方のスイッチをOFFにすることのできる状態を持ちます。バッファはこのために用意された要素です。"Z"状態か論理出力状態（"0"状態か"1"状態）をコントロールするための信号入力をイネーブル(enable)と言います。右下に様々なバッファの例を示します。
　慣習的に、"Z"(ハイ・インピーダンス High Impedance)状態のことをトライ・ステート(3-state)状態と呼ぶ場合があります。

【図４】バッファ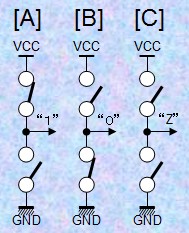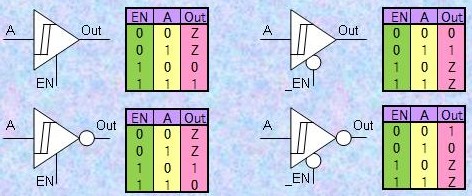
　　
 
　ところで、バッファ・デバイスの中にはグランド側にスイッチを１つしか持たないオープン・コレクタ(O.C.)あるいはオープン・ドレイン（O.D.)というデバイスもあります。これは下図のようにCPUの割込みのように複数のデバイスのうちどれか１つでも割込み状態が発生した場合に通知する/INTラインや右図のようにLEDを点灯させる場合などに使います。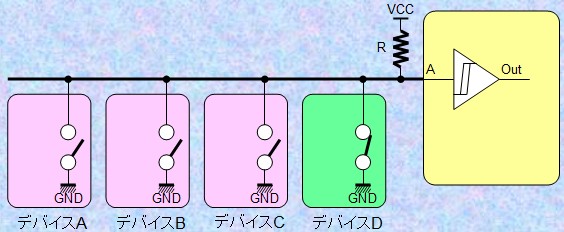
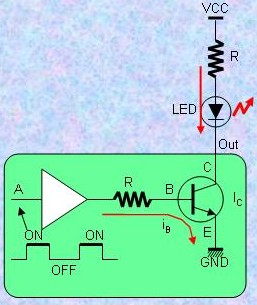
1.5) AND (論理積)
　正論理ではある条件が成立している状態を"1"で示します。
　ANDは入力となるすべての条件が同時に成立していることを示すロジック・デバイスです。
　ANDは「全ての入力が"1"のときのみ"1"を出力」します。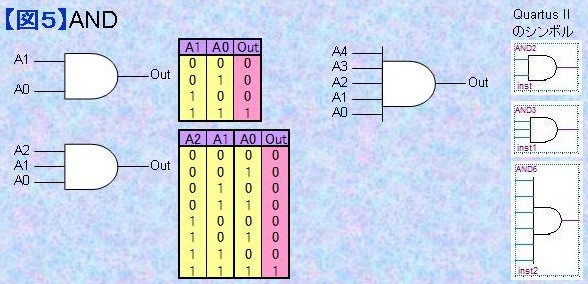
1.6) NAND
　NANDはANDの出力に論理の反転を示す白丸マーク○が付いています。
　従って、「入力のすべての条件が同時に成立していないとき"1"」を示すデバイスですが、頭の中ではANDを考えてからその論理を反転すればOKです。
　もしくは、白丸マーク○を条件が成立したとき"0"を出力すると考えてください。
　NANDは「全ての入力が"1"のときのみ"0"を出力」します。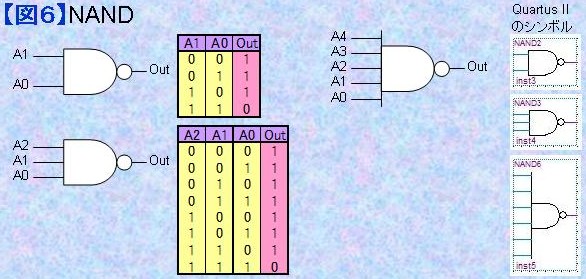　
1.7) OR (論理和)
　ORはいずれか１つの条件が成立しているデバイスです。
　つまりORは「いずれか１つの入力が"1"のとき"1"を出力」します。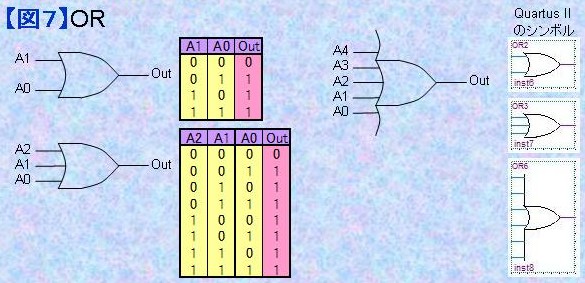
1.8) NOR
　NORはORの出力に白丸マーク○が付いているのでORの出力を反転しているデバイスです。
　つまりNORは「いずれか１つの入力が"1"のとき"0"を出力」します。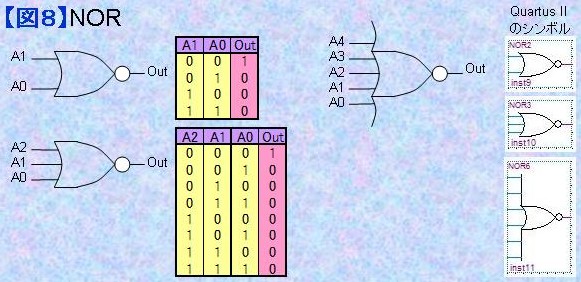
1.9) XOR (Exclusively OR 排他的論理和)
　XOR (Exclusively OR)は排他的論理和と呼ばれますが、わかりやすく考えれば２進数の足し算に当たります。
　　０＋０＝０
　　０＋１＝１
　　１＋０＝１
なのはすぐわかりますよね？では１＋１はどうでしょうか？
１０進数なら１＋１＝２ですが、２進数では桁上がりを起こして10Bになるのでこの桁は０になります。
つまり
　　１＋１＝０
　　ｃｙ←１
です。
XORは桁上がりを無視した特定桁部分だけの演算（加算）結果を示すデバイスであると考えます。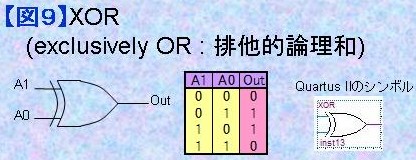　　
1.10) XNOR
　XNORはXORの出力に白丸マーク○が付いているので、XORの出力を反転した論理ですが、次のようにも考えられます。
　●「入力が一致したことを示す」デバイス
　●いずれか一方の入力を反転してXORに入力している。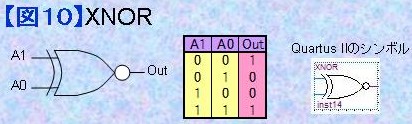

　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　等価論理の例
1.11) VCCとGND（グランド）
　CPLDやFPGAに予め用意されたライブラリには該当する入力数のゲートがない場合や使わない入力を"1"または"0"の論理状態に固定したい場合があります。具体的には５入力を持ったNANDを使いたいのに、ライブラリには４入力NANDか６入力NANDしかない場合があります。このようなときは使わないピンを"1"に固定しなければなりません。対象がANDでも同じです。OR、NORの場合には未使用ピンは"0"に固定する必要があります。このような場合に回路図を用いた設計では図１１に示すようなVCC("1")あるいはGND("0")のシンボルを使います。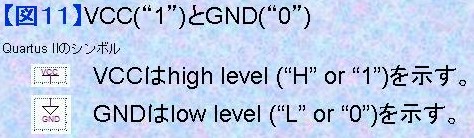
1.12) 論理の等価変換法について (ド・モルガンの公式)
 　回路図による設計をしていると複雑な論理になってしまう場合が多々あります。こんなときには図１２のような変換が成立します。数学的には「ド・モルガンの公式」を使うことになり、一見複雑なようですが、言葉とは便利です。
　「入出力とも反転して、論理積と論理和を入れ替える」
だけです。
　このような変換を使うと、右下図のように一見複雑ように見えた論理も実は３入力のAND１つで済むことがわかります。このように少ない論理デバイス数になるように行う論理変換をreduceと呼びます。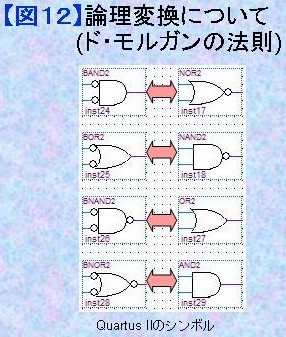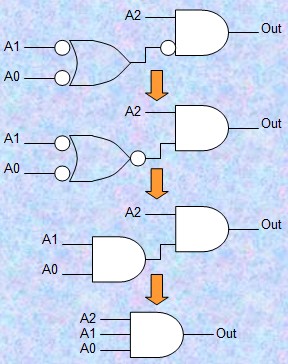

　　　　
1.13) 入出力ピン
　CPLDあるいはFPGAの論理開発ツールではICの入出力ピンに対応させて図１３のシンボルを使います。それ以外にも、階層構造でライブラリや回路ブロックを作る場合に入出力にピンのシンボルを使います。



特にライブラリや回路ブロックを記述する場合にデータやアドレスのように複数ビットがまとまった入力(バス・ライン)となっている場合には次のようにします。
　例： ピン名称をname[23..0]のように記述します。
       nameという名称の24本のバスでbit0からbit23の信号線

●16bitレジスタのピン使用例
1.14) ピンとバッファ
　CPLDあるいはFPGAのロジック設計においては、論理レベル(入出力電圧と内部ロジック電圧)の変換を行う必要があるため、必ず入出力バッファを介して接続を行う必要があります。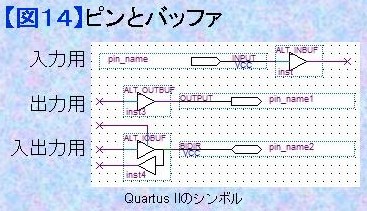
　
1.15) デコーダ (decorder)
　アドレスやデータが特定の値を示した場合のみ反応させたい場合があります。このような場合はANDあるいはNANDロジックを使うことで簡単に実現できます。このとき、入力が"1"で条件成立させたい場合は直接入力させ、入力が"0"で成立させたい場合は白丸マーク○[論理の反転]を付け加えます。
　図１５はA[5..0]＝001010BのときCS＝"1"とする場合の事例です。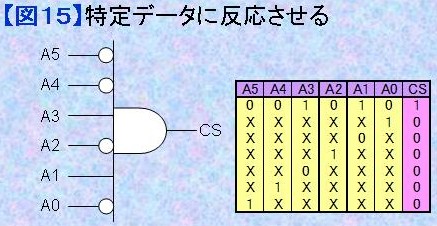

　図１６の事例は入力状態のすべての組み合わせに対して出力を出すデコーダ回路の例です。
ANDあるいはNANDの入力に白丸マーク○の付いている入力は"0"のときに反応し、白丸マーク○が付いていない入力は"1"のときに反応することを示します。このように回路図(シンボル)設計は式設計と違って直感的に理解しやすいメリットがあります。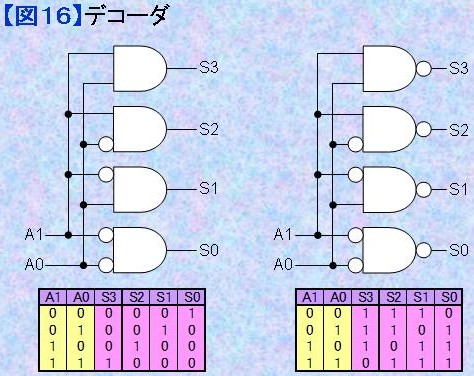
２．INV-AND-OR-treeを理解せよ！
　CPLDあるいはFPGAのロジック設計で最も重要な要素のひとつがINV-AND-OR-treeです。単体で様々な演算を実現することができます。また、レジスタと組み合わせることでクロックと同期して動作する様々な部品を構成することができます。本章では演算要素の説明を行います。		 　
2.1) セレクタ
　図１７左側に２入力１出力のセレクタの構成例を示します。A入力はSが"0"のとき、B入力はSが"1"のとき選択出力されます。ANDは入力の１つが"0"であれば出力が必ず"0"となるため、ｎ入力ANDのn-1本の入力を選択条件、残り１入力を選択信号入力とします。図１７左側は２入力ANDの例なので白丸マーク○が付いている方は"0"のとき選択されます。
　図１７右側は４入力１出力のセレクタの例です。３入力ANDを使っているので、２入力が選択条件として使われています。選択条件が成立しているANDだけが選択された入力信号をそのままの論理でORに出力するのに対して選択条件が成立していないANDの出力は常に"0"となります。その結果、後段のORからも選択信号が出力されます。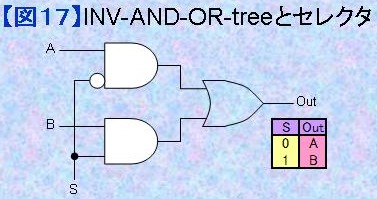

　　　　　
2.2) プライオリティー・エンコーダ
　プライオリティー・エンコーダとは信号に優先順位を設けて、優先順位に対して与えられたコードを出力するデバイスです。図１８のプライオリティー・エンコーダはA,B,Cの３入力があり、最も優先順位が高い信号がA、次に優先順位の高い信号がB、最も優先順位の低い信号がCです。A,B,Cとも"0"のときはどのANDも選択されず、"0"を出力するので、出力コードはY[2..0]＝０ですが、A＝１なら一番上のANDのみ選択されて"1"を、他は"0"を出力するのでY[2..0}＝５を出力します。A＝０でB＝１なら真中のANDのみ選択されて"1"を出力、上と下のANDは"0"を出力するのでY[2..0]＝３となります。A＝０、B＝０、C＝１なら下のANDのみ選択されるのでY[2..0]＝１となります。
　このようにANDはプライオリティーを判断する目的で、ORはプライオリティーに対応するコードを出力するために使われています。ORへの結線先を変更することで出力するコードを変更することができます。
　プライオリティー・エンコーダはCPUの割込み信号や割込みに対応する割込みベクトルを発生するためによく用いられる部品です。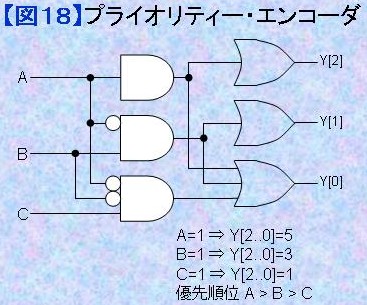　
2.3)  XORとINV-AND-OR-tree
　図１９に示すように1.9)で述べたXOR (exclusively OR 排他的論理和)は実はINV-AND-OR-treeで構成することができます。２つのANDはそれぞれ真理表の中央２段のロジックに対応しています。A0＝０、A1＝１のとき上側が、A0＝１、A1＝０のとき下側が選択されORに"1"を出力します。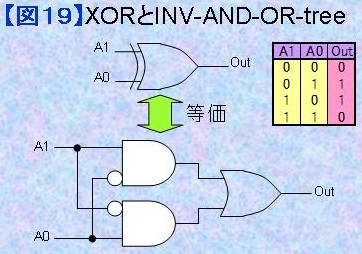
2.4) 加算器 (Adder)
　1.9)で述べたようにXOR単体では２進数の加算を意味します。桁上がり(キャリー carry)を考慮するには図２０のようにします。ｎ桁目の加算はAnとBnの加算をXORで求めた後で、ひとつ下からの桁上がり信号Cn-1を考慮して２つめのXORを使って計算しDnを得ます。
　さらに上位桁への桁上がり信号CnはAn＝１かつBn＝１のときか、An＝１かつCn-1＝１のときか、あるいはBn＝１かつCn-1＝１のときに発生します。つまり上位桁への桁上がり信号Cnの発生はAND-OR-treeで行えることがわかります。2.3)でも述べましたがXORも上位桁への桁上がり信号の発生もINV-AND-OR-treeの応用であることがわかるでしょう。
　複数ビット幅の加算演算を行う場合には図２０左側の演算ブロックをカスケード接続によって実現できることがわかると思います。しかし、この方式には欠点もあります。つまり下位桁の桁上がり側の演算が終了しないと桁上がりを考慮した演算を行うことができないのです。高速な回路を設計したい場合にはこのようなカスケード接続法は極めて不利となります。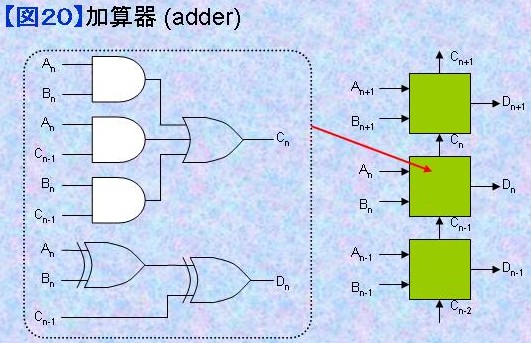
2.5) 高速加算器を作るためのキャリー・ルック・アヘッド回路 (Carry Look Ahead)
  2.4)の加算器ではカスケード段数(演算ビット幅)が多いとキャリー(桁上がり信号)の遅延による演算速度の低下現象が顕著です。
そこで、加算演算速度を高速化する方法として、下位桁の情報を一度に全て使ってｎ桁目に入力するキャリーを演算するキャリー・ルック・アヘッド回路を紹介します。以下に示すように２桁目へのキャリーC0はG0, P0, C-1によって与えられるのでこれを順次上の桁のキャリーを求める式に代入していくことでAND-OR-treeで各桁のキャリーを求めることができることがわかります。この方式だと、どの桁もほぼ同時に自分の桁へのキャリーを演算することができるのでカスケード方式と比べて高速に加算演算を行うことができます。
　さらに2.4)で示したように加算演算そのものはXORを２個使って、An＋Bn、その演算結果＋Cnの２段階で演算されるため、後述のレジスタを使ってパイプライン化することによって見かけの演算速度を倍速にすることもできます。
2.6) インクリメント (increment)
　入力の値を＋１することをインクリメント(increment)すると言います。その演算器はインクリメンタと呼ばれます。
「各桁の値が変化するのはそれより下位の桁がすべて"1"の場合だけ」なので、図２１に示すように簡単に＋１の結果を求めることができます。。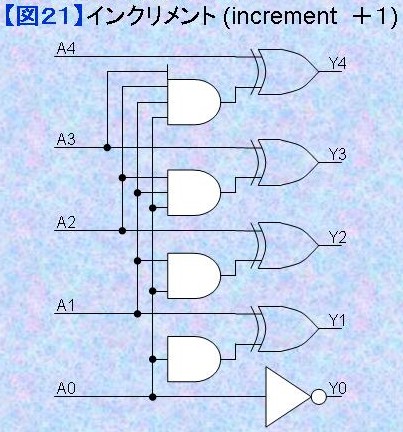
2.7)　ディクリメント (decrement)
　入力の値を－１することをディクリメント(decrement)すると言います。その演算器はディクリメンタと呼ばれます。
「各桁の値が変化するのはそれより下位の桁がすべて"0"の場合だけ」なので、図２１のANDの入力に白丸マークを入れて図２２のようにすることで簡単に－１の結果を求めることができます。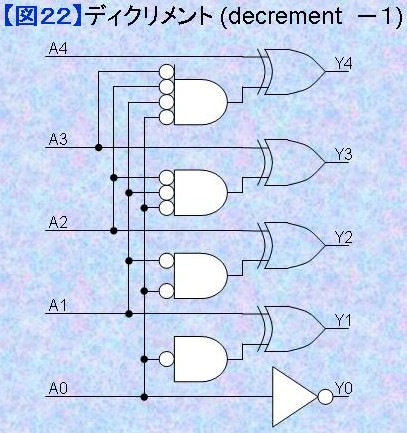
３．レジスタの活用
　ここからは、状態を保存しながら機能を持ったファンクションを実現するために必要な事項を紹介します。
繰り返しになりますが、CPLDあるいはFPGAのロジック設計において重要なことはINV-AND-OR-treeとレジスタを如何に組み合わせるかという点にあります。本章では、同期式アップ/ダウン・カウンタやシフト・レジスタ、ステート・マシンの構成方法について述べます。
3.1) RSフリップ・フロップ
　図２３にNANDゲート２個からなる回路を示す。この回路はRSフリップ・フロップ（R-S Flip Flop）と呼ばれる。２つの負論理入力/R (/リセット)と/S (/セット)を持ち、通常は両入力とも状態"1" (Higjh Level)としておく。
　今、入力/R (/リセット)側を状態"0"(Low Level)にする。するとNANDゲートPのもう片方の論理が状態"X"(don't care :"0"であれ、"1"であれ)でも出力状態は"1"となる。するとNANDゲートQの２つの入力はともに状態"1"となるのでゲートQの出力は状態"0"となる。回路は出力Qは"0"、出力/Qは"1"の状態で安定する。
　入力/R (/リセット)側を状態"1"(High Level)に戻しても、回路全体の状態に変化はなく、出力Qは"0"、出力/Qは"1"の状態を維持する。しかも、入力/R (/リセット)側の状態が再び状態"0"となっても回路全体の状態に変化はない。
　次に、入力/R (/リセット)側が状態"1"(High Level)に戻っている状態で、入力/S (/セット)側を状態"0"(Low Level)とすれば、ゲートQの片方の入力が"0"となったことでゲートQの出力は"1"となり、続いてゲートPの入力はともに"1"となるのでゲートP出力は"0"となる。回路は出力Qは"1"、出力/Qは"0"の状態で安定する。
　入力/S (/セット)側を状態"1"(High Level)に戻しても、回路全体の状態に変化はなく、出力Qは"1"、出力/Qは"0"の状態を維持する。しかも、入力/S (/セット)側の状態が再び状態"0"となっても回路全体の状態に変化はない。
　以上のようにRSフリップ・フロップ（R-S Flip Flop）は入力/R (/リセット)の"1"→"0"→"1"で出力Qを０にリセット(クリア)し、入力/S (/セット)の"1"→"0"→"1"で出力Qを１にセット（プリセット）する。しかも入力に変化がないかぎり、状態を維持し、記憶することができる。
　論理変換を使えばNORゲート２個でも同様の機能の回路を構成することができる。

　RSフリップ・フロップ（R-S Flip Flop）はチャタリング除去や回路の初期化等で使用されることが多い。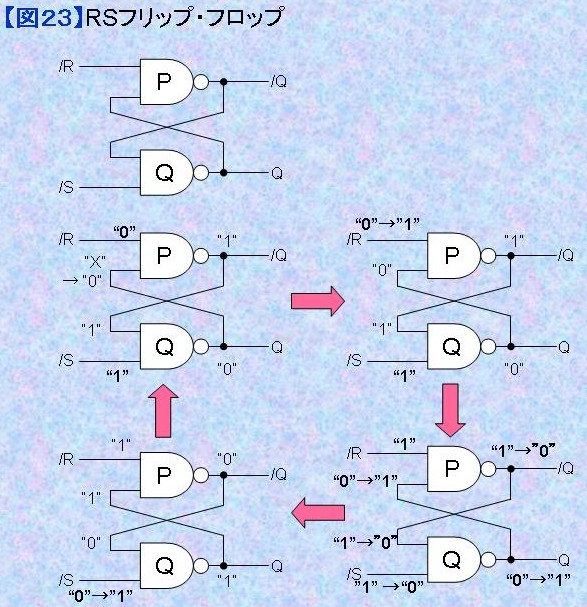

 注）状態が"0"でも"1"でもかまわないという状態はdon't care (かまわない)と呼び、"X"と表記する。
3.2) レジスタとラッチ (RegisterとLatch)
　状態を記憶する機能要素はストレージ(storage)と呼ばれる。CPLDあるいはFPGAの設計ツールを使用する限り、上記RSフリップ・フロップを使用することは稀である。他に代表的ストレージ要素としてはレジスタとラッチがあるが、結論から先に言えばレジスタだけ利用できればそれで十分である。
　図２４にレジスタとラッチのシンボルを例示する。
　レジスタはクロック入力(CK)の立ち上がりエッジ(↑)で、入力Dの状態を記憶(保持：　hold)する機能要素であり、ラッチはゲート（G)がON (状態"1" : High Level)のときは入力Dをそのまま出力し、ゲート(G)がOFF (状態"0" : Low Level)となった瞬間の入力Dの状態を記憶(保持：　hold)する機能要素である。
　レジスタとラッチの動作の違いを示す回路シミュレーション結果を下に例示する。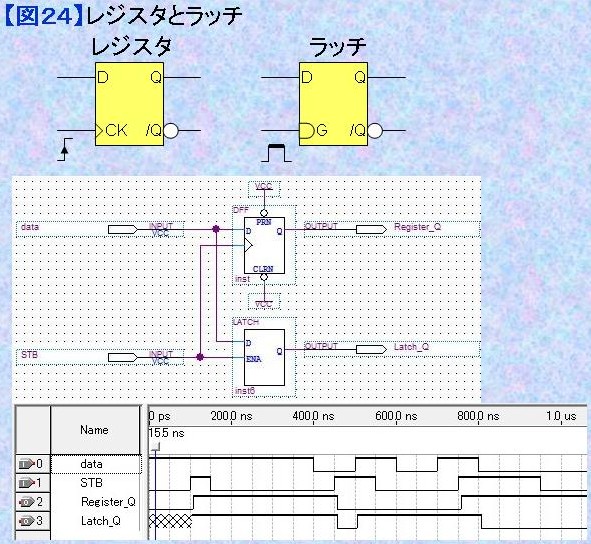
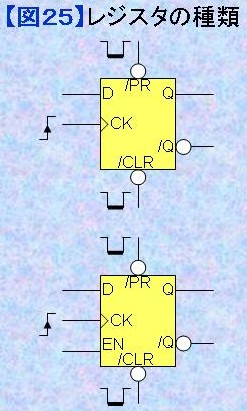
3.3) レジスタのバリエーション
　Altera社のCPLD/FPGA向け無償開発ツールQuartus II Web Editionの場合、primitiveと名付けられた機能要素が提供されている。ストレージ(storage)関連要素だけでもDフリップ・フロップ(レジスタ)、ラッチ、JKフリップ・フロップ、RSフリップ・フロップ、Tフリップ・フロップと多彩だが、一体何を使えばよいのか？初心者には混乱をもたらす原因ともなる。
　基本的にレジスタさえ使えれば回路設計上、困ることはない。図２５にdffとdffeに対応したシンボルを示す。実際のQuartus II Web Editionのライブラリに収納されているレジスタには/Q出力はなく、Q出力のみである。図２４に示したレジスタの入力D、クロックCK、出力Q以外に、非同期入力の/CLR (/クリア)と/PR (/プリセット)入力を持っている。これらは共に負論理入力で通常未使用時は"1"に保つ必要がある。入力/CLR (/クリア)を状態"0" (Low Level)にするとクロックに関係なく、フリップ・フロップは強制的にゼロ・クリア(状態"0")される。また、入力/PR (/プリセット)を状態"0" (Low Level)にするとクロックに関係なく、フリップ・フロップは強制的にプリセット(状態"1")される。また、イネーブル入力(EN)を持ったレジスタもある。
　入力ENを持たないレジスタ (ｄｆｆ)は、クロックの立ち上がりエッジ(↑)で入力Dの状態を保持(ホールド)するが、入力ENを持ったレジスタ (dffe)は、ENが状態"1"のときにクロックが立ち上がったときのみ入力Dの状態を保持(ホールド)し、ENが状態"0"のときにクロックが立ち上がっても記憶状態は変化しない。　
3.4) 非同期カウンタとその欠点
　経過した時間を精密に計測したり、パルスの数を高速にカウントする場合にはカウンタが利用される。図２６にレジスタの/Q出力を入力Dにフィードバックしたダウン・カウンタを例示する。Quartus IIのライブラリに収納されたレジスタdffの場合には/Q出力がないため、Q出力をインバータ(NOT）で反転させて入力Dに戻す。また、/CLR (CLRN)と/PR (PRN)は使わないのでVCCと接続して状態"1"に保つ。
　図２６のカウンタはクロックの立ち上がりエッジ(↑)が入るタイミングで状態を反転していく。Q[3]を23桁、Q[2]を22桁、Q[1]を21桁、Q[0]を20桁と考えれば、シミュレーション結果からわかるようにクロックの立ち上がりエッジ毎に値が0000B⇒1111B⇒1110B⇒1101B⇒1100B⇒1011B⇒1010B⇒1001Bとダウン・カウントしてゆく。
　しかし、シミュレーション結果を良く見ると、このカウンタの欠点に気が付く。
　どのようなデバイスも演算結果を出力するまで遅れ時間を伴う。
　このカウンタは各桁のクロックを一つ下の桁の値の変化で作っているので、上位の桁程、遅延時間が累積し、シミュレーションの例でも数ナノ秒ずつ遅れて変化する。各桁が同時に変化しないので、遅延が上位桁に伝搬している時点でデータを読み込むと変化前の上位桁の状態を読み込む結果となり、正しいカウント値を読み込むことができないのである。
　この遅延問題は高速のカウンタを実現したい場合に特に顕著となる。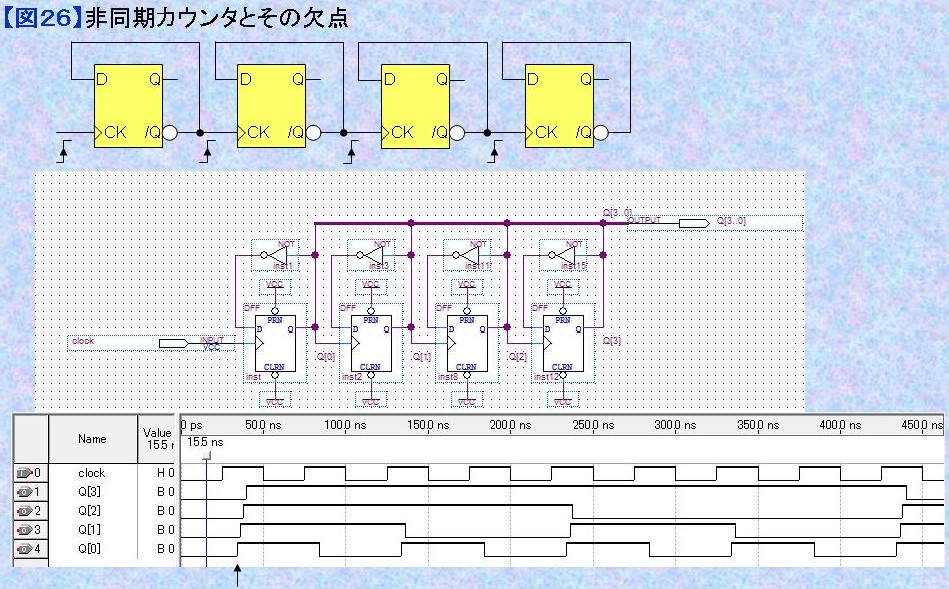
3.5) 同期式カウンタ（アップ・カウンタとダウン・カウンタ）
　図２７に１つのシステム・クロックに同期して各桁の変化を同時に発生させる同期式アップ・カウンタの回路図を例示する。アップ・カウンタはそれより下位桁のQ値がすべて"1"のとき桁上がり条件が成立してQ値を反転させることになる。これを反転条件という。反転条件はANDによって作ることができる。上位桁ほど多くの下位桁のQ値のANDを取ることになる。なお、最下位桁だけは常にクロックの立ち上がりエッジ毎に反転するので、常に反転条件は"1"となる。
　各レジスタの入力Dに接続されたINV-AND-OR-treeはセレクタとなっている。反転条件が非成立(状態"0")ならQ値を反転させず、反転条件が成立(状態"1")ならQ値を反転させる。なお、最下位桁だけは常にクロックの立ち上がりエッジ毎に反転するので、セレクタ部分の回路は大幅にreduceされてインバータ(NOT)のみになる。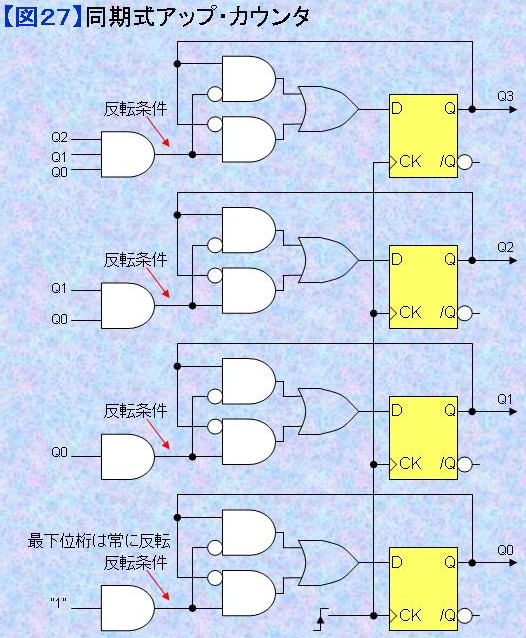

　図２７に同期式ダウン・カウンタの回路を例示する。回路はアップ・カウンタとほとんど同じである。ダウン・カウンタではレジスタの値の反転条件が下位桁がすべて"0"になることである。ANDの入力には反転のためのインバータが入れられている。
　以上のことから、アップ/ダウンを切り替えるのは反転条件を取り換えるだけでよいことがわかると思う。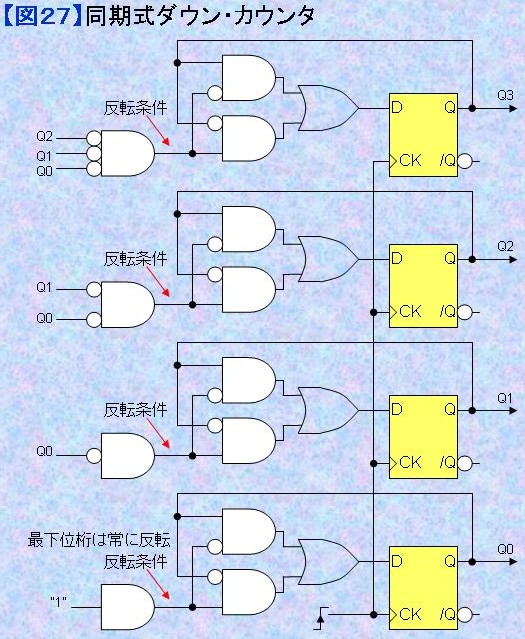
3.6) シフト・レジスタの構成法とその用途
　図２８にシリアル入力/パラレル出力のシフト・レジスタの回路図を例示する。
構成は単純であるが、SPIインターフェースの受信回路、調歩同期式シリアル受信回路の一部等に幅広く使用されている。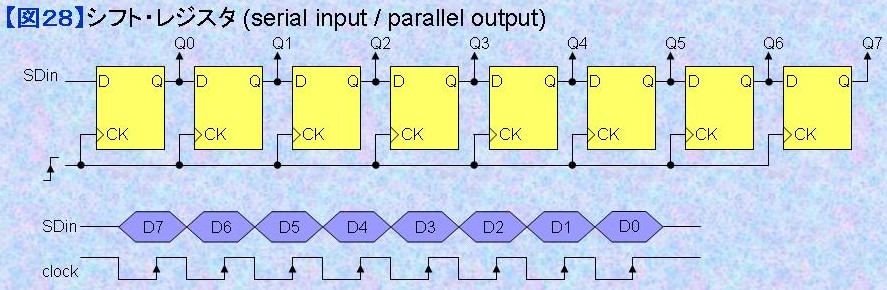
　図２９にパラレル入力/シリアル出力のシフト・レジスタの回路図を例示する。
レジスタにパラレル入力するときは入力選択条件となる入力Load/_Shift信号を状態"1"とする。クロックの立ち上がりエッジで入力Dnからレジスタにデータをロードする。入力Load/_Shift信号を状態"0"としてクロックを入れるたびに左シフトあるいは右シフトを行う。
　２進数で１ビットの左シフトと行うとデータの値は２倍となる。ｎビットの左シフトは２ｎ倍と同じである。
　反対に、２進数で１ビットの右シフトと行うとデータの値は1/2倍となる。ｎビットの左シフトは２-n倍と同じである。
　一般的な掛け算器（乗算器）や割り算器(除算器)の回路規模は大きいが、２ｎ倍や２-n倍の演算を行う回路の規模は非常に小さい。
　他の用途としては、SPIインターフェースのシリアル送信回路、調歩同期式シリアル通信回路の送信回路、グラフィック表示のビデオ出力部等に幅広く使われる。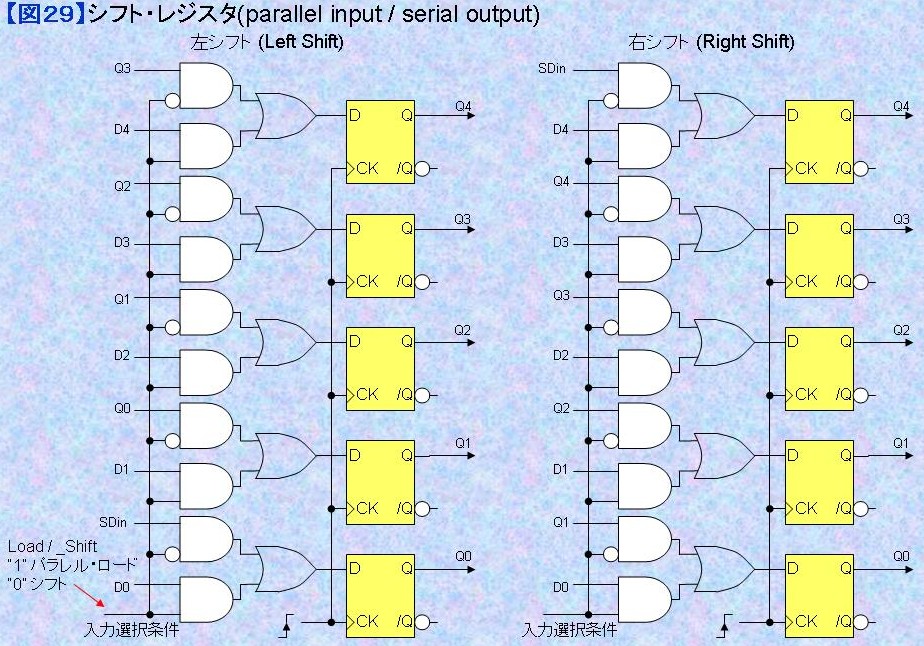
3.7) ステート・マシン
　図３０に最も原始的なステート・マシンの構成要素の回路図を例示する。このステート・マシンはクロックに同期して状態遷移を行う。レジスタの状態を"1"にすることでそのステート(状態)になったことを示す。レジスタの状態が"0"のときはそのステートではないことを示す。
　そのステートに入り込む条件をincome条件と言い、そのステートから離脱する条件をoutcome条件と言う。
図３１のようにincome条件やoutcome条件が複数個ある場合にはORを使う。必要に応じて、ORの前に各条件の詳細条件をデコードするためのINV-ANDを設ける。
　誤動作を避けるため、図３１のstate3へのincome条件A (あるいはstate1からのoutcome条件A)は少なくとも、
　　　income条件A　：　(state1=1) AND (入力信号の状態＝予め定められた状態A')
であるべきであり、同様に
　　　income条件B　：　(state3=1) AND (入力信号の状態＝予め定められた状態B')
　　　income条件C　：　(state1=1) AND (入力信号の状態＝予め定められた状態C')
　　　income条件D　：　(state2=1) AND (入力信号の状態＝予め定められた状態D')
であるべきである。
　しかし、この方法では、少なくともステート数だけのレジスタが必要となる。つまり、１個のLE (Logic Element)に１つしかレジスタは割り当てられないので、図３１の例では少なくとも３個のLE (Logic Element)が必要とされる。

【図３０】ステート・マシンの機能要素　　　　　　　　　　　　　　　　【図３１】状態遷移図の例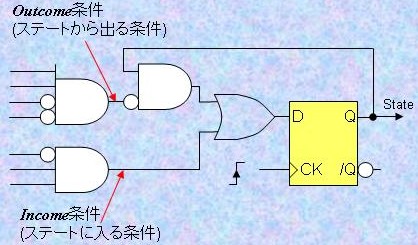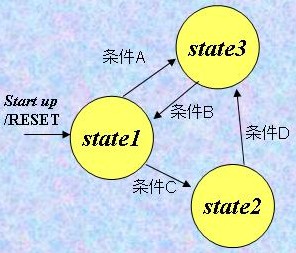　


【図３２】図３１に対応した実施例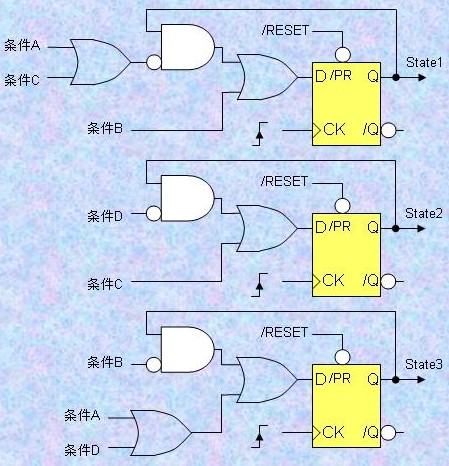


　ロジックを圧縮してLE (Logic Element)を節約するには、ｎ個のレジスタで２ｎ個のステートを表現する。
　図３１の例では合計３個のステートしかないので２個のレジスタを用いる。上記の例題は以下のような状態に設定する問題に変換される。
      state1  :     Reg[1]=0,   Reg[0]=0
      state2  :     Reg[1]=0,   Reg[0]=1
      state3  :     Reg[1]=1,   Reg[0]=0
　図３０のステート・マシンのincome条件 をレジスタ状態を"1"にするset条件に、outcome条件をレジスタ状態を"0"にするreset条件に読み替えるだけで上記の仕様に変換することができる。
　　Reg[0]のset条件は、Reg[0]=1となる(income）条件を示すので、state2になる条件Cのみである。
　　Reg[0]のreset条件は、Reg[0]=0となる(income）条件を示すので、state1またはstate3になる条件A,B,Dである。
　　Reg[1]のset条件は、Reg[1]=1となる(income）条件を示すので、state3になる条件A,Dである。
　　Reg[1]のreset条件は、Reg[1]=0となる(income）条件を示すので、state1またはstate2になる条件B,Cである。
　誤動作をさけるため、
　　条件A　：　Reg[1]=0 AND Reg[0]=0 AND (入力信号の状態＝予め定められた状態A')
　　条件B　：　Reg[1]=1 AND Reg[0]=0 AND (入力信号の状態＝予め定められた状態B')
　　条件C　：　Reg[1]=0 AND Reg[0]=0 AND (入力信号の状態＝予め定められた状態C')
　　条件D　：　Reg[1]=0 AND Reg[0]=1 AND (入力信号の状態＝予め定められた状態D')
とする。

　ステート・マシンはビデオ同期信号のタイミングを作る場合やマイコンでは応答できない高速の判定を行う場合などに用いる。

【あとがき】
 　　本編では、ディジタル系計測回路の試作において、頻繁に登場する回路ブロック（ボキャブラリと呼んでいます。）の基本構成要素の動作原理を 理解することに的を絞った解説を行いました。CPLDやFPGAのロジック開発は、INV-AND-OR-treeとレジスタの組み合わせ方法によっていると言っても過言ではありません。CPLDやFPGAのロジック開発ツールには基本的なマクロが殆ど用意されていますが、高速な回路や安定性を重視した回路開発を行うためにはこれらの基本回路を理解していることが重要です。デバイスを最高速で動かそうとすれば、HDL（Hardware　Design Language）で設計する場合でも、回路図設計を行う場合でもロジックを突き詰めて考える必要があります。また、そのロジックをデバイスのどこに配置するかさえ、遅延時間を詰めるために重要になってきます。